Pendahuluan
Komponen terkecil dalam Ilmu Bahasa (Linguistik) yang memiliki makna spesifik dikenal dengan istilah morfem. Aronof (2005:2) mengemukakan bahwa morfem sering didefinisikan sebagai bagian terkecil dari linguistik yang memiliki fungsi gramatikal. Bidang Ilmu yang mengkaji morfem adalah morfologi. Bidang ilmu ini mengkaji struktuk dan bentuk atau formasi dari morfem. Dengan kata lain morfologi mengkhususkan diri pada analisa struktur dan bentuk sebuah morfem yang sedang dikaji.
Berdasarkan prosesnya, Yule (2010) membagi proses morfologi ke dalam 5 bagian yaitu proses afiksasi, komposisi, reduplikasi, akronimisasi, dan proses penyerapan. Apabila ditinjau dari objeknya, kelima proses morfologi tersebut melibatkan morfem-morfem dalam tingkatan kata atau frase, sementara pada tingkat huruf, sebagai unsur dasar pembentuk morfem, tidak terlibat ke dalam kelima proses morfologi tersebut. Hal ini seolah-olah menisbikan peran fundamental huruf sebagai unsur dasar pembentuk morfem. Bahkan pada tataran bidang yang lebih sempit dari morfologi yaitu fonologi (ilmu bunyi) tidak melibatkan huruf secara keseluruhan sebagai objek fundamentalnya. Sebagaimana pendapat Chaer (2009) yang mengatakan bahwa fonologi mengkaji bunyi bahasa sebagai satuan terkecil dari ujaran, maka berdasarkan pendapat tersebut, dapat disimpulkan bahwa objek dasar dari fonologi adalah huruf vocal karena hanya huruf vocal yang dapat dibunyikan oleh alat bicara atau artukulasi bunyi pada manusia. Sehingga huruf konsonan sebagai salah satu penyusun dasar morfem tidak termasuk sebagai objek dasar fonologi. Hal ini mengakibatkan adanya kesenjangan antara fonologi sebagai ilmu bunyi dan morfologi sebagai ilmu struktur dan bentuk morfem.
Barangkali untuk mengatasi kesenjangan tersebut, perlu dikonstruksi sebuah kerangka kerja atau framework sebagai tempat untuk menuangkan dan menganalisa masalah-masalah linguistic khususnya terkait permasalahan morfem dan lain-lain.
Dalam artikel ini akan diperkenalkan kerangka kerja yang dimaksudkan di atas. Wujud atau bentuk dari kerangka kerja tersebut berupa matriks (Adiwijaya, 2014) yang dikreasikan dengan cara operasi bak-pinor. Adapun konsep bak-spinor merupakan analogi dari spinor dalam fisika kuantum yaitu elemen ruang vector berbasis bilangan kompleks yang bertansfomasi secara linier (Hermann, 1966). di Kemudian analisa linguistic dapat di lakukan dengan menggunakan konsep Fisika Kuantum dan Matematika.
Metode
Penelitian ini menggunakan metode tinjauan pustaka. Adapun jenis pustaka yang digunakan adalah terkait konsep linguistic (khususnya morfem), konsep matematik (khususnya konsep matriks), dan konsep fisika kuantum (khususnya konsep bak-spinor).
Pada artikel ini, morfem dianalogikan sebagai objek fisis dalam fisika kuantum, baik sebagai partikel dasar maupun partikel komposit. Selanjutnya, jenis operasi matriks yang digunakan untuk mengkonstruksi framework adalah operasi pada bak-spinor, baik perkalian-dalam maupun perkalian-luar (Gusnedi, 1999). Adapun jenis bak-spinor dibagi menjadi dua bentuk yaitu berbentuk kolom (ruang ket) dan berbentuk baris (ruang bra) (Gidney, 2017). Misalnya, untuk bak-spinor dasar yang disajikan dalam di Ruang Ket dapat disajikan berikut ini,
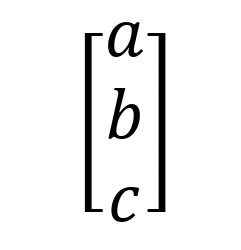
Berbeda dengan bak-spinor yang disajikan ke dalam bentuk baris, yaitu
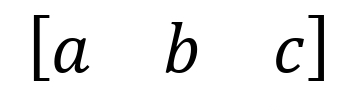
Untuk mempermudah penulisan ruang ket disimbolkan dengan I⋯⟩ dan ruang bra disimbolkan dengan ⟨⋯I
Ruang representasi morfem dibentuk dengan melibatkan operasi perkalian luar I⋯⟩⟨⋯I (dibaca ketbra).

Hasil operasi Ketbra ditunjukkan oleh matriks (m,n) berikut ini.

Gambar 1. Matriks Ruang Representasi Morfem
Dengan m adalah baris matriks dan n adalah kolom matriks. Matriks (m,n) merepresentasikan ruang representasi morfem yang dihasilka dari operasi ketbra bak-spinor Ket dan bak-spinor Bra. Setiap entri (unit cell) dari matriks representasi mewakili sebuah morfem. Dari ruang representasi tersebut dapat dilihat bahwa terdapat 676 buah bakal calon morfem yang dibangkitkan oleh operasi perkalian luar ruang Ket dan uang Bra (Braket).
Matriks ruang representasi morfem terdiri dari matriks segitiga atas dan matriks segitiga bawah yang dipisahkan oleh diagonal matriks ruang representasi (warna kuning). Matriks segitiga bawah merupakan cermin atau bayangan dari matriks segitiga bawah dan berlaku juga sebaliknya. Misalnya, cell [23,5] (we) memiliki cermin atau bayangan [5.23] (ew) dan berlaku sebaliknya.
Analisa Linguistik Morfem
1. Jenis morfem yang dibangkitkan
Dalam matriks ruang representasi morfem, dapat diketahui bahwa terdapat beberapa jenis morfem yang dibangkitkan dari operasi Ketbra. Adapun jenis morfem tersebut adalah morfem bebas (warna hijau atau bayangannya), morfem terikat (warna biru atau bayangannya), dan morfem yang berupa akronim.
2. Karakter atau properties morfem
Setiap morfem di dalam ruang representasi memiliki cermin atau bayangan. Antara morfem dan bayangannya memiliki sifat antisimetri baik dari segi struktur maupun dari segi makna. Misalnya, morfem on memiliki bayangan berupa morfem no yang mana memiliki struktur yang berbeda dan makna yang berbeda pula. Tidak semua morfem dalam ruang representasi morfem memiliki bayangan yang berupa morfem yang sejenis. Misalnya, morfem or adalah morfem bebas sementara bayangannya morfem ro bukan morfem bebas tetapi morfem yang berupa akronim atau tidak mewakili morfem manapun di dalam bahasa inggris. Khusus untuk morfem yang berada di diagonal matriks memiliki karakter special yaitu bayangan morfem adalah dirinya sendiri. Misalnya, morfem ww memiliki bayangan yang sama dengan dirinya yaitu ww.
3. Pembangkitan morfem
Pembangkitan atau penciptaan morfem secara alami dapat dilakukan melalui proses perkalian luar yang melibatkan bak-spinor Ket dan bak-spinor Bra. Morfem yang dibangkitkan dapat diambil atau diadopsi oleh bahasa atau rumpun bahasa tertentu, misalnya Bahasa Inggris.
Ruang representasi morfem juga dapat dikonstruksi dengan melibatkan operasi perkalian dalam ⟨⋯I⋯⟩ (dibaca braket).

Operasi perkalian dalam Braket yang melibatkan bak-spinor bra < a | dan bak-spinor Ket | ad > menghasilkan morfem tunggal add. Jadi, operasi Braket yang melibatkan bak-spinor Bra dan bak-spinor Ket akan menghasilkan morfem tunggal.
Hasil dan Pembahasan
Pada penelitian ini, telah berhasil diproduksi matriks yang memuat morfem yang selanjutnya disebut matriks ruang representasi morfem. Selain itu juga, melalui proses operasi Braket, Ruang representasi morfem diproduksi dalam bentuk ruang skala (non-matriks) yang memuat morfem tunggal. Adapun mekanisme produksi ruang representasi morfem telah dijabarkan pada bab sebelumnya.
Adapun penelitian tentang morfem sejauh ini masih dalam ruang lingkup analisis objek yang sudah tersedia (God given). Adapun ruang lingkup kajian terkait morfem adalah perubhan struktu dari morfem yang meliputi afiksasi, reduplikasi, dan komposisi (Subroto, 1991; Vehaar, 1987: 52-64; Sudaryanto, 1991:15). Berbeda dengan penelitian yang disajikan dalam artikel ini, dengan metode atau kaidah matriks dan konsep dasar fisika quantum terkait bak-spinor dan operasi perkalian pada bak-spinor, peneliti dapat membangkitkan morfem dari unsur terkecil dari kata yaitu huruf. Hasil pembangkitan tersebut diperoleh ruang repesentasi morfem. Dengan menggunakan ruang representasi tersebut, sifat atau karakter dari morfem dapat diuraikan secara jelas. Misalnya morfem memiliki sifat asimetri terhadap cemin atau bayangan dari morfem tersebut baik dari segi struktur maupun maknanya.
Kehadiran ruang representasi morfem, baik dalam bentuk ruang matriks maupun ruang scalar, dapat memberik kemudahan dalam menganalisa morfem yang dimuatnya. Selain itu juga, dengan memperkenalkan ruang representasi morfem yang berbentuk objek matematis atau fisis dapat memberi pintu masuk bagi analisator linguistic untuk menggunakan konsep-konsep matematika dan konsep fisika yang relevan. Dengan kata lain, kehadiran ruang representasi morfem dapat memperkuat atau mendukung peran sains dalam memecahkan masalah-masalah bahasa khususnya masalah linguistic.
Analisa morfem tentu bergantung pada jenis bahasa yang sedang ditinjau. Sehingga hasil analisa sifat morfem dari ruang representasi dapat menghasilkan kesimpulan yang berbeda untuk kajian morfem dengan tinjauan bahasa yang berbeda. Meskipun demikian, ruang representasi morfem yang dihasilkan tidak bergantung pada jenis bahasa yang akan ditinjau. Jadi, ruang representasi morfem dapat berlaku secara general.
KESIMPULAN
Penelitian ini telah berhasil membangkitkant atau memproduksi ruang representasi morfem yang dapat berupa ruang matriks atau ruang scalar. Keberadaan ruang representasi tersebut dapat membantu dalam mengkaji morfem dari poses pembangkitan hingga proses analisa karakter atau sifat morfem tersebut. Disamping itu juga, ide tentang ruang representasi morfem sebagai framework atau kerangka kerja dalam mengkaji atau menganalisis morfem dapat menjadi salah satu motivasi untuk mengembangkan ilmu linguistic yang melibatkan bidang sains terutama bidang Fisika maupun matematika.
Untuk penelitian yang akan datang, perlu melibatkan bak-spinor yang lebih kompleks dalam operasi Ketbra atau Braket. Sehingga dapat diketahui kemampuan ruang representasi morfem dalam membangkitkan, memuat dan menyajikan morfem serta kompatibel terhadap proses morfologis.
REFERENSI
Aronoff, M. dan Fudeman, K. 2005. What is Morphology. Australia: Blackwell Publishing.
Yule, George. 2000. Pragmatics. Berlin. Oxford University Press.
Chaer, Abdul.2009. Pengantar Semantik Bahasa Indonesia. Jakarta: PT Rineka Cipta.
Adiwijaya, Kang. 2014. Aplikasi Matriks dan Ruang Vektor.
Hermann. 1966. The Theory of Spinors. Paris
Gusnedi. 1999. Matriks dan Ruang Vektor. DIP Universitas Negeri Padang.
Gidney, Craig (2017). Bra–Ket Notation Trivializes Matrix Multiplication.
Sudaryanto. 1992. Tata Bahasa Baku Bahasa Jawa. Yogyakarta: Duta Wacana University Press.
Subroto, Eddi D., dkk. 1991. Tata Bahasa Deskriftif Bahasa Jawa. Jakarta: Depdikbud.
Verhaar, JWM. 1987. Pengantar Linguistik. Yogyakarta:Gadjah Mada University Press.
